r**2 - r0**2
Gm(r) = K'**2 ----------------- (magnitude)
(r**2 + r0**2)**2
Gp(r) = tan-1(r/r0) (phase)
/ r**2 - r0**2 \
Gr(r) = K' sqrt( ----------------- ) sin(tan-1(r/r0)) (real component)
\(r**2 + r0**2)**2/
/ r**2 - r0**2 \
Gi(r) = K' sqrt( ----------------- ) cos(tan-1(r/r0)) (imaginary component)
\(r**2 + r0**2)**2/
This is the simplest function that meets the required criteria. K' is a proportionality constant K, times the mass. The constant r0 is for now, an arbitrary constant, and establishes the radius of the sphere defining the SOE.
Consider 2 such functions acting on each other at a distance. In the presense of an intrinsic opposition to curvature, the difference in the rate of change in the ambient G, across its SOE, will accelerate the SOE towards the side of greater ambient G. The equivalent force will be this acceleration times the mass. The acceleration can be computed as the difference in the rate of change of G times a constant, R, which is proportional to the intrinsic resistance to curvature and which normalizes the results to the units of distance. This constant will be derived in Part 4 of the proof.
To compute forces in this way, we first need to compute dG(r)/dr. For r >> r0, the sin(tan-1(r/r0)) term becomes 1 and can be ignored for now and the imaginary component becomes 0, thus we can take the derivative of just the real component.
u = r**2 - r0**2
v = r**2 + r0**2
dG(r) K' / v**2 \ 1
----- = - * sqrt(--------) * ----- * (2vr - 4ur)
dr 2 \ u / v**3
dG(r) / 1 \ r
----- = K' * sqrt(----------------) * ----------------- * (3r0**2 - r**2)
dr \(r**2 - r0**2)/ (r**2 + r0**2)**2
For r >> r0, this can be simplified to,
dG(r) 1 r
----- = K' * - * ----- * (-r**2)
dr r r**4
dG(r) -K'
----- = ----
dr r**2
Solving for forces to account for the motions resulting from the computed actions results in a 1/r**2 force relationship where the gravitational constant can be expressed in terms of the curvature constant K, which adjusts for units of mass, distance and time, and the resistance constant R which quantifies the Universes resistance to curvature.
Compute the acceleration as the difference in the rate of change in the ambient curvature across the SOE. For 2 particles interacting along a line, this can be computed as the difference in the dg/dr product at the 2 points of the SOE along the vector connecting the interacting masses. The sum is used in the calculation since the sign of the slopes at r=r0 and r=-r0 are opposite of each other. In other words, both sides push towards the center and one side pushes harder than the other, resulting in a net motion and apparent force.
dG(r+r0) dG(r-r0)
A(r) = -R(-------- + --------)
dr dr
1
A(r) = K'R * ---------------------
(r+r0)**2 + (r-r0)**2
1
A(r) = K'R * -----------------
2r**2 + 2**r0**2
For r >> r0, the effect of the r0**2 terms goes to zero resulting in,
K'R 1
A(r) = --- * ----
2 r**2
Previously, we defined K' to be the mass times the constant K and the equivalent force is the mass times the acceleration. Assuming the 2 interacting particles are the same mass and substituting, we can compute the equivalent force as,
K R m**2
F(r) = --- * ----
2 r**2
From this relationship, we can see that if the gravitational constant G is equal to KR/2, then the gravitational forces computed based on CTE considerations are the same as the forces computed with classical gravitational equations.
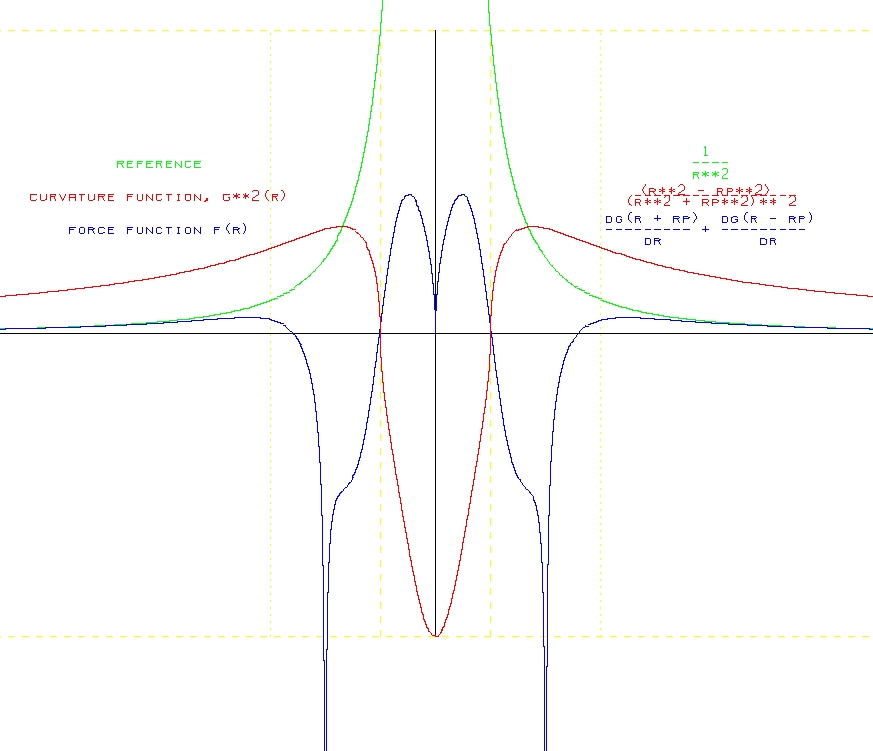
Forces based on this curvature function have been simulated and a plot of the calculated force and the corresponding curvature is shown below. The red line is the magnitude squared of the curvature function, the blue line is the effective force as computed by the above force function. The green line is a reference 1/x**2 curve. At small distances, there is a large repulsive force which at smaller distances becomes a large attractive force. The exact quantification at small distances may not be correct as the simulation currently only accounts for the magnitude of the curvature. At small distances, it does appear to have the same basic characteristics as the strong force, although the sign may be incorrect due to incorrectly accounting for the phase and/or imaginary component of the curvature at distances close to r0 (the plot labels this as rp instead of r0). This needs more work in order to more precisely quantify the strong force. It is interesting that the transition is at r0, which should make r0 quantifiable from strong force arguments.

Part 4 quantifies the resistance of the Universe to curvature and determined the constants K and R.
(C) 1997-2004 George White, All Rights ReservedCTE Home, Doc map