A controversial concept in climate science is what fraction of incremental GHG absorption affects the surface temperature. HITRAN based simulations confirm that the IPCC stated radiative forcing of 3.7 W/m² is the incremental absorption from doubling CO2, but climate alarmism assumes that all of this affects the surface, while physics requires that only half does.
The physical proof considers the atmosphere as a black box (not to be confused with a black body) with inter-related boundary conditions. At the top boundary, 239 W/m² of post albedo solar power enters and 239 W/m² of radiated power leaves. This power flux corresponds to the 255°K equivalent temperature of the Earth and is known to be strictly radiative. At the bottom boundary, the surface at 287°K radiates 385 W/m², which must be replaced with the same amount of power entering the surface from the bottom of the atmosphere.
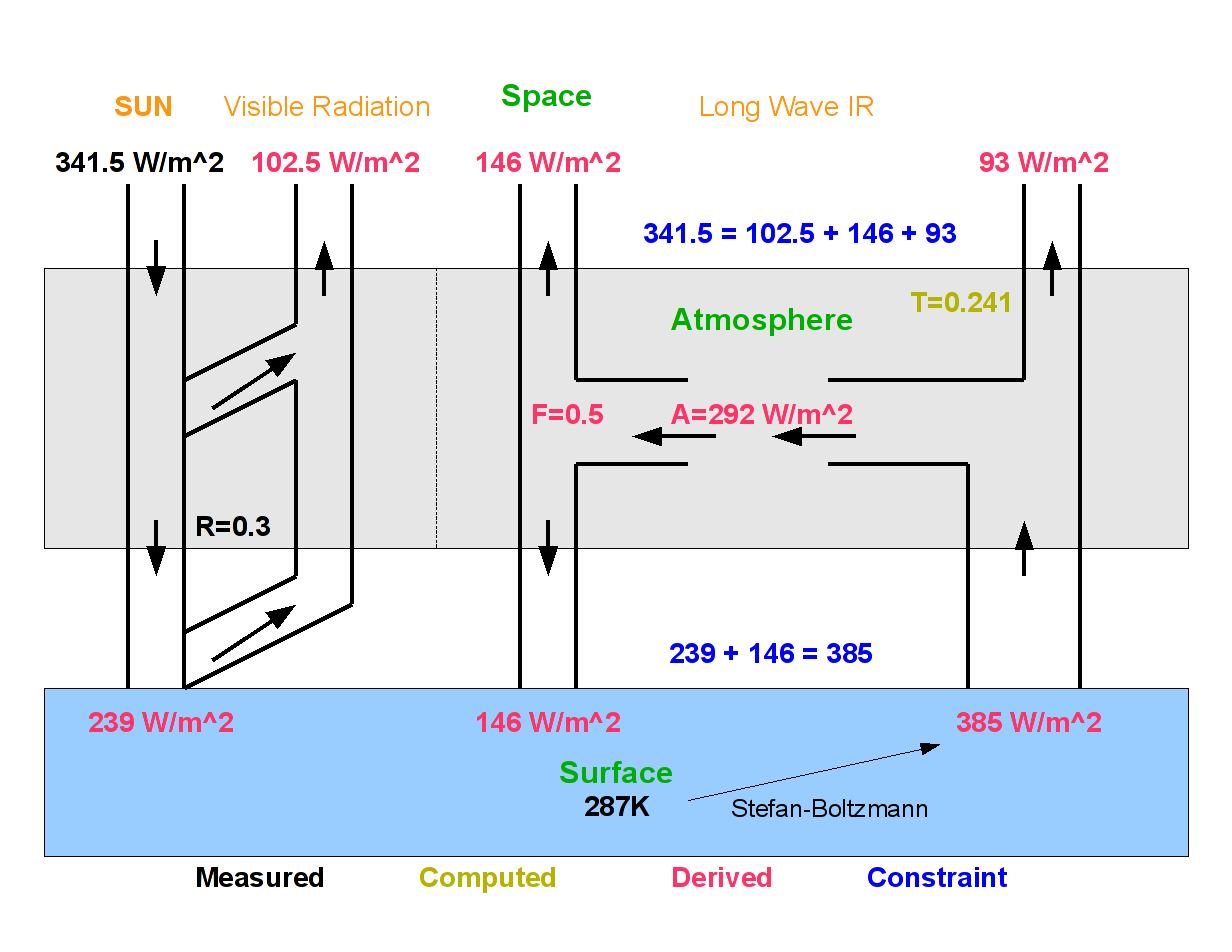
The picture at right shows the relationships between all of the radiative fluxes relevant to the radiative balance. The average surface temperature, average incident solar power, average albedo and size of the transparent region of the atmosphere are inputs and everything else is deterministically derived as described below. Of these, only the size of the atmospheric window is not a measured value. This is calculated from 3-d, HITRAN driven, atmospheric simulations based on nominal GHG concentrations and nominal cloud coverage, and at 24.1%, is not that far away from the 18% estimated by Trenberth et all, 2009.
You should notice that only radiation components are included and non radiative components, like latent heat and thermals, are not. Relative to the radiative balance, the only thing that matters is EM radiation. The non radiative components act primarily to redistribute and reorganize the energy stored in the Earth's thermal mass, specifically, as fluxes in and out and within the thermal mass spanning the oceans and atmosphere, including atmospheric and oceanic circulation currents. A condition on the altitude of the lower atmospheric boundary is that it must separate the thermal mass from the atmosphere. Setting this boundary to be coincident with the surface is only approximately true, but none the less, the total heat capacity of the atmosphere is a tiny fraction of the heat capacity of the planet making this a reasonable approximation. A further constraint of Conservation Of Energy is that the global net non radiative flux between the atmosphere and the surface must be zero in the steady state if the radiative flux is also zero. While radiative flux to and from the surface can be traded off against non radiative flux, it makes no difference to the overall radiative balance.
Since the atmosphere creates no energy of it's own, these boundary conditions can be expressed as,
T
239 = T*385 + (1-F)*A
385 = 239 + F*A
A = 385*(1-T)
This is a redundant set of equations, thus there is no unique solution despite 3 equations and 3 unknowns, however, given values of T between 0 and 239/385 (0.622), a unique value of F always exists. If we solve for F and consider 4 values of T, 0.18, 0.22, 0.24 and 0.26, the behavior of the solution space becomes evident. The 0.18 value is shown to match the Trenberth estimate of atmospheric absorption.
A = 385*(1-T)
F = 146/A
T = 0.18 -> A = 316, F = .462
T = 0.22 -> A = 300, F = .486
T = 0.24 -> A = 293, F = .499
T = 0.26 -> A = 285, F = .512
Note that based on Trenberth's atmospheric absorption model, less than half of the absorbed power must be sent to the surface, not more! This is a consequence of more radiation required by the atmosphere to make up the difference between power passing through the transparent window and the required emitted power.
From the physics of black bodies, the atmosphere should behave as an isotropic radiator with half of it's emitted power going up and half down, thus we can say that the transparent window of the atmosphere must be about 24% since physics dictates that F must be one half. While this is a valid approach, another is to arrive at this from the other direction and calculate the size of the transparent window from HITRAN based simulations to see what F should be based on calculated absorption.
Simulations say that the clear sky absorbs about 62% of the surface power, for a transparent window spanning 38% of the emitted power spectrum. The cloudy sky absorbs between 62% and 100% of the surface power, for an average is 83%, corresponding to an average transparent window of 17%. From ISCCP data, the average cloud coverage is 66%, so the cloud fraction weighted size of the transparent atmospheric window is, 0.66*0.17 + (1-0.66)*0.38 = 0.241, whose corresponding value of F is 0.500, as expected.
This confirms that the physics of black body radiators predicts the average transparency of the atmosphere and that both measurements and atmospheric simulations confirm that within 1%, only half of the power absorbed by the atmosphere affects surface temperatures.
As a falsification test, consider the implication of a net atmospheric opacity limited to 50%. Even if all of the surface power is absorbed, half will still escape into space. This can be tested by measuring the ratio of the power emitted by the coldest cloud tops and the surface power beneath them. Again, the ISCCP data tells us that for 100's of thousands of gridded measurements spanning decades across the entire globe, cloud power asymptotically approaches half of the surface power and on average is about 2/3 of the surface power, as shown in the diagram to the right.
Why is the counter example of Venus so different? Because the thermal mass of Venus is primarily dense, energized CO2 in the atmosphere above the surface, while on Earth, the primary thermal mass is ground state water in the oceans below the surface and it's this thermal mass which is the focus of energy entering and leaving the system upon which surface temperature and the emitted surface power depends.
In conclusion, there can be no question that only half of all absorption by the clear and cloudy atmosphere, GHG or otherwise, affects the surface, moreover; quantifying the energy balance in terms of atmospheric opacity provides the precise mechanism for how incremental absorption affects surface temperatures. The consequence of this is that everything claimed by the IPCC must be reexamined.